| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Integral Iterada de Seis Modos Diferentes https://forumdematematica.org/viewtopic.php?f=10&t=4612 |
Página 1 de 1 |
| Autor: | raimundojr [ 15 dez 2013, 19:41 ] |
| Título da Pergunta: | Integral Iterada de Seis Modos Diferentes |
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 32 - Pág.: 921) Expresse a integral \(\iiint_E f(x, y, z)dV\) como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. x=2, y=2, z=0, x+y-2z=2 |
|
| Autor: | João P. Ferreira [ 16 dez 2013, 17:14 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
caro, como calcula não lhe vamos colocar aqui os seis modos diferentes  está perante uma pirâmide de base quadrangular na prática repare que tem seis combinações para fazer os integrais \(\iiint dxdydz\) \(\iiint dxdzdy\) \(\iiint dydzdx\) \(\iiint dydxdz\) \(\iiint dzdxdy\) \(\iiint dzdydx\) |
|
| Autor: | raimundojr [ 16 dez 2013, 21:41 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
É o mesmo que 3!=6 (lê-se: três fatorial), pois equivale a uma permutação simples de 3 elementos (os elementos aqui são os três diferenciais). Gostaria mesmo da análise dessa integral postada dos seis modos diferentes, porque gostaria de ver também a análise feita para cada domínio da integral tripla, mesmo assim obrigado. Integral Tripla: \(\iiint_B f(x, y, z)dxdydz\) B: é o "conjunto domínio" sobre o qual irá ser feita a integração. |
|
| Autor: | João P. Ferreira [ 17 dez 2013, 00:39 ] | ||
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes | ||
Caro amigo o objetivo do fórum não é resolver grupos de exercícios todavia dou-lhe aqui uma boa dica vai em anexo figura do volume de integração e já dois integrais calculados dúvidas diga, estamos aqui para ajudar...
|
|||
| Autor: | raimundojr [ 17 dez 2013, 22:39 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
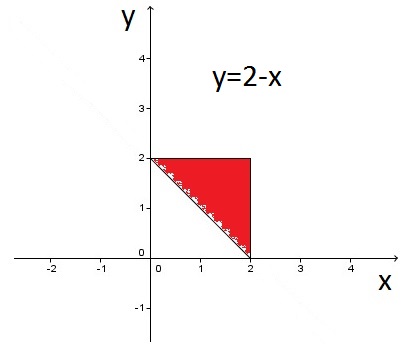
Obrigado por responder. Prezado amigo, não leve a mal. Porém, se eu soubesse responder a pergunta (quando a publiquei), nem teria me dado o trabalho de postá-la. Então, às vezes, gostaria de uma resposta mais objetiva do que ser escrito algo já conhecido (ou óbvio). Obtive as integras abaixo. Poderia confirmar o resultado diferente de algumas? Às integrais: Plano xy: (1)\(\int_{0}^{2}\int_{2-x}^{2}\int_{0}^{\frac{x+y-2}{2}} f(x, y, z)dzdydx\) Em (1) deve ter considerado o "triângulo abaixo do gráfico", na verdade, é o que está acima. (2)\(\int_{0}^{2}\int_{2-y}^{2}\int_{0}^{\frac{x+y-2}{2}} f(x, y, z)dzdxdy\) Confira dzdydx postado anteriormente. 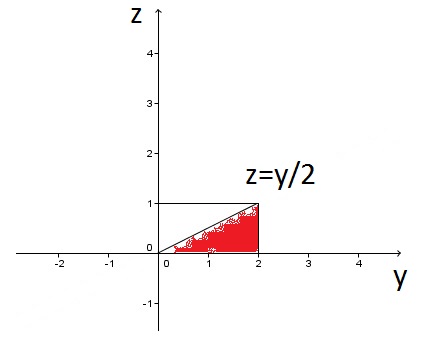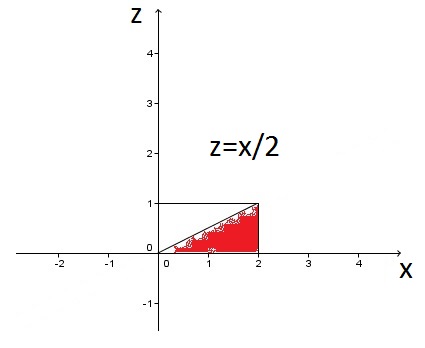Anexo: 01.jpg [ 12.79 KiB | Visualizado 4367 vezes ] Plano yz: (3)\(\int_{0}^{2}\int_{0}^{\frac{y}{2}}\int_{2z-y+2}^{2} f(x, y, z)dxdzdy\) (4)\(\int_{0}^{1}\int_{2z}^{2}\int_{2z-y+2}^{2} f(x, y, z)dxdydz\) Anexo: 02.jpg [ 11.93 KiB | Visualizado 4367 vezes ] Plano xz: (5)\(\int_{0}^{2}\int_{0}^{\frac{x}{2}}\int_{2z-x+2}^{2} f(x, y, z)dydzdx\) (6)\(\int_{0}^{1}\int_{2z}^{2}\int_{2z-x+2}^{2} f(x, y, z)dydxdz\) Anexo: 03.jpg [ 11.82 KiB | Visualizado 4367 vezes ] |
|
| Autor: | João P. Ferreira [ 18 dez 2013, 10:46 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
Caro Raimundo Perdão, nâo quis ser rude, mas aparece ás vezes aqui cada coisa, que por vezes ficamos algo extenuados Sim, tem toda a razâo, fiz mal aquele primeiro integral os seus outros integrais parecem-me estar certíssimos, pelo menos executou muito bem o pensamento, tendo estruturado as ideias de como abordar o problema Já agora, vejo que percebe de matemática, é muito bem-vindo a ajudar a comunidade search.php?search_id=unanswered um abraço
|
|
| Autor: | raimundojr [ 18 dez 2013, 19:08 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
Muito obrigado e agradeço o convite. |
|
| Autor: | João P. Ferreira [ 19 dez 2013, 14:29 ] |
| Título da Pergunta: | Re: Integral Iterada de Seis Modos Diferentes |
de nada, sempre ao dispôr atentamente |
|
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|