Estudo da Natureza das Séries
15 jan 2011, 01:45
Estudar a Natureza das Séries:
Obrigado João
Obrigado João
Re: Estudo da Natureza das Séries
17 jan 2011, 15:47
Epah... tantas de uma vez 
1 - A primeira é divergente e podes usar as séries de Dirichlet para demonstrar que séries do género
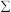 (n>=1, 1/n^(a)) são divergentes para a <=1. Logo a série é divergente.
(n>=1, 1/n^(a)) são divergentes para a <=1. Logo a série é divergente.
2 - Na segunda série usas o critério da comparação, considerando que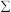 (1/n^2) converge e que 1/n^2 > 1/(n^2+1). Logo esta série converge
(1/n^2) converge e que 1/n^2 > 1/(n^2+1). Logo esta série converge
3 - A terceira série converge e podes usar o critério D'Alambert ou da razão. Ou seja: lim u(n+1)/u(n) = 0, como este limite é zero, a série converge
As outras ainda vou pensar, relembra-me para te resolver as outras mais tarde.
Grande abraço e qq dúvida coloca aqui.
Fica bem André
1 - A primeira é divergente e podes usar as séries de Dirichlet para demonstrar que séries do género
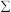 (n>=1, 1/n^(a)) são divergentes para a <=1. Logo a série é divergente.
(n>=1, 1/n^(a)) são divergentes para a <=1. Logo a série é divergente.2 - Na segunda série usas o critério da comparação, considerando que
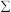 (1/n^2) converge e que 1/n^2 > 1/(n^2+1). Logo esta série converge
(1/n^2) converge e que 1/n^2 > 1/(n^2+1). Logo esta série converge3 - A terceira série converge e podes usar o critério D'Alambert ou da razão. Ou seja: lim u(n+1)/u(n) = 0, como este limite é zero, a série converge
As outras ainda vou pensar, relembra-me para te resolver as outras mais tarde.
Grande abraço e qq dúvida coloca aqui.
Fica bem André
Re: Estudo da Natureza das Séries
17 jan 2011, 16:30
4 - A quarta série não converge e podes demonstrá-lo pelo critério d'Alambert ou da razão pois
lim u(n+1)/u(n)=Inf
5 - A quinta série também diverge e podes usar o critério da raiz ou seja
lim (u(n))^(1/n) > 1. Logo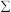 (4^n*n!)/n^n é divergente
(4^n*n!)/n^n é divergente
lim u(n+1)/u(n)=Inf
5 - A quinta série também diverge e podes usar o critério da raiz ou seja
lim (u(n))^(1/n) > 1. Logo
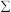 (4^n*n!)/n^n é divergente
(4^n*n!)/n^n é divergente
Re: Estudo da Natureza das Séries
17 jan 2011, 17:29
Muito obrigado pela ajuda..
 Um abraço..
Um abraço..
Re: Estudo da Natureza das Séries
17 jan 2011, 17:36
De nada 
qq dúvida aparece por aqui
qq dúvida aparece por aqui