Fórum de Matemática | DÚVIDAS? Nós respondemos!
https://forumdematematica.org/

Progressões, Somatório, Indução Matemática e Convergência de Sucessões
https://forumdematematica.org/viewtopic.php?f=22&t=8965		 Página 1 de 1
Autor:  Dita Silva [ 08 jun 2015, 09:41 ]
Título da Pergunta:  Progressões, Somatório, Indução Matemática e Convergência de Sucessões
Bom dia,
Encontrei um livro de exames da minha mãe e achei que era uma boa maneira de me preparar para o exame, deparei-me com o seguinte exercício:

Considere a sucessão de numeros reais de termo geral:
\(\sum_{k=1}^{n} a^{-2k}, a\epsilon \mathbb{R}^{+}\\setminus 1\)

1- Mostre por indução matemática que

Anexo:
Comentário do Ficheiro: Esta é a demonstração que nos pedem por indução matemática
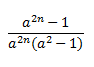
duvida.PNG
duvida.PNG [ 827 Bytes | Visualizado 2659 vezes ]


2- Estude, em função de a, a convergência da sucessão.

Este livro tem resoluções mas eu não percebo como é que eles misturam o somatório com a indução nem me lembro de como se estuda a convergência,

Podem ajudar-me por favor? É urgente!
Obrigado :)
Autor:  TelmaG [ 20 jun 2015, 18:04 ]
Título da Pergunta:  Re: Progressões, Somatório, Indução Matemática e Convergência de Sucessões
Olá Dita

\(\large \sum_{k=1}^{n}\, a\, ^{-2k}\) designa uma soma (somatório) em que todas as parcelas são do tipo \(\large a\, ^{-2k}\) onde k designa um número natural que varia de 1 até n , isto é, trata-se da soma dos primeiros n números naturais (que estão em progressão geométrica)

A soma dos n primeiros termos de uma progressão geométrica é dada por \(\LARGE u\, _{1}\times \frac{1-r\, ^{n}}{1-r}\) e por se tratar de uma progressão geométrica temos que \(\large \frac{u\, _{n+1}}{u\, _{n}}=r\) e ainda \(\large u\, _{1}=a\, ^{-2}\)

\(\LARGE \sum_{k=1}^{n}\, a\, ^{-2k}=a\, ^{-2}\times \frac{1-\left (\frac{a\, ^{-2\left ( n+1 \right )}}{a\, ^{-2n}} \right )^{n}}{1-\frac{a\, ^{-2\left ( n+1 \right )}}{a\, ^{-2n}}}=\frac{1}{a\, ^{2}}\times \frac{1-\frac{1}{a\, ^{2n}}}{1-\frac{1}{a\, ^{2}}}=\frac{1}{a\, ^{2}}\times \frac{a\, ^{2n}-1}{a\, ^{2n}}\times \frac{a\, ^{2}}{a\, ^{2}-1}=\frac{a\, ^{2n}-1}{a\, ^{2n}\left ( a\, ^{2}-1 \right )}\)
Página 1 de 1 Os Horários são TMG [ DST ]
Powered by phpBB® Forum Software © phpBB Group
https://www.phpbb.com/