| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Equação geral de uma reta https://forumdematematica.org/viewtopic.php?f=23&t=10116 |
Página 1 de 1 |
| Autor: | dante312 [ 14 dez 2015, 17:34 ] |
| Título da Pergunta: | Equação geral de uma reta [resolvida] |
Achar a equação da reta que passa pelo ponto B(5,-5) e que forma com os eixos de coordenadas um triângulo de 50 unidades de área. |
|
| Autor: | Fraol [ 14 dez 2015, 18:48 ] |
| Título da Pergunta: | Re: Equação geral de uma reta |
Você pode raciocinar assim (diretamente): Uma reta que satistaz o ponto \(B(5,-5)\) é \(r: y = x -10\). Nessa equação se \(x=0\) então \(y = -10\) e se \(y=0\) então \(x=10\). Então teríamos um triângulo com vértices \((0,0)\), \((10,0)\) e \((0,-10)\) (retângulo em \((0,0)\)) cuja área é \(50u\). |
|
| Autor: | jorgeluis [ 14 dez 2015, 20:50 ] |
| Título da Pergunta: | Re: Equação geral de uma reta |
se o ponto B(5,-5) está no 4o quadrante, então, podemos dizer que, partindo da origem A(0,0) a reta passa pelo ponto B(5,-5) até chegar em \(C(\sqrt{50}, -\sqrt{50})\) determinando o coeficiente angular pelo ponto B: \((y - y_o) = m.(x - x_o) (5 - 0) = m.(-5 - 0) m = -1\) agora, determinando a equação geral da reta pelo ponto C: \((y - y_o) = m.(x - x_o) (\sqrt{50} - y) = -1.(\sqrt{50} - x) x + y - 2.\sqrt{50} = 0\) |
|
| Autor: | Fraol [ 15 dez 2015, 00:05 ] |
| Título da Pergunta: | Re: Equação geral de uma reta |
Boa noite, Vendo a interpretação do colaborador jorgeluis resolvi montar uma imagem para ilustrar a minha interpretação acima: (a propósito: jorgeluis a sua equação não comporta o ponto B, certo?) Anexo: triang.png [ 10.79 KiB | Visualizado 2380 vezes ] |
|
| Autor: | jorgeluis [ 15 dez 2015, 15:40 ] | ||
| Título da Pergunta: | Re: Equação geral de uma reta | ||
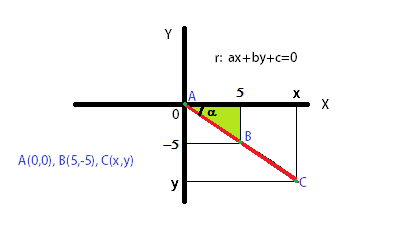
Fraol, você está certo, a área definida no intervalo dos pontos A(0,0) e B(5,-5) é: \(S=\frac{\Delta x.\Delta y}{2}=\frac{(5-0).(-5-0)}{2}=12,5ua\) logo, para uma área de 50 ua suas dimensões \(\Delta x\) e \(\Delta y\) devem ser aumentadas em 100%. Assim, o ponto C(x,y) fica C(10,-10): \(S=\frac{\Delta x.\Delta y}{2}=\frac{(10-0).(-10-0)}{2}=50ua\) achando a Equação Geral da Reta pela determinação do coeficiente angular, temos: \((y-y_o) = m.(x-x_o) (-10-y) = -1.(10-x) x + y = 0\) r: x + y = 0 a reta passa pela origem, por isso: c=0
|
|||
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|