| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Confusão dificil envolvendo seno conseno t tangente https://forumdematematica.org/viewtopic.php?f=23&t=10352 |
Página 1 de 1 |
| Autor: | habakuk.conrado [ 30 jan 2016, 02:07 ] | ||
| Título da Pergunta: | Confusão dificil envolvendo seno conseno t tangente | ||
Considere o quarto de um círculo de raio 1 e os triângulos ABE e ACD apresentados na figura a seguir. Utilizando fórmulas de área padrão para concluir que: (1/2)*senx*cosx<x/2<(1/2)*senx/cosx
|
|||
| Autor: | Fraol [ 30 jan 2016, 14:52 ] |
| Título da Pergunta: | Re: Confusão dificil envolvendo seno conseno t tangente |
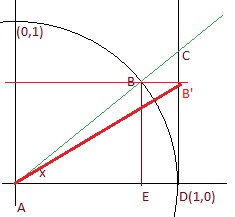
Olá, Usei a sua figura para implementar um triângulo auxiliar ADB': Anexo: adsas.jpg [ 12.9 KiB | Visualizado 1067 vezes ] Pode-se ver que a área de AEB é menor do que a área de ADB' pois os dois triângulos têm a mesma altura mas a base do segundo é maior. Assim: \(\frac{1}{2} \cdot AE \times EB = \frac{1}{2} \cdot cos(x) \cdot sen(x) < \frac{1}{2} AD \cdot DB' = \frac{1}{2} \cdot 1 \cdot sen(x) .\) Também pode-se ver que a área de ADB' é menor do que a área de ADC pois os dois triângulos têm a mesma base mas a altura do segundo é maior. Assim: \(\frac{1}{2} \cdot AD \times DB' = \frac{1}{2} \cdot 1 \cdot sen(x) < \frac{1}{2} AD \cdot DC = \frac{1}{2} \cdot 1 \cdot tg(x) = \frac{1}{2} \cdot 1 \cdot \frac{sen(x)}{cos(x)}.\) Dessa forma eu mostrei que \(\frac{cos(x) \cdot sen(x)}{2} < \frac{sen(x)}{2} < \frac{sen(x)}{2cos(x)}\). Eu não consegui mostrar o seu termo do meio (\(\frac{x}{2}\)). Para isso, usando a minha abordagem, só chegaria em \(\frac{sen(x)}{2}= \frac{x}{2}\) para valores de \(x\) muito próximos de 0. |
|
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|