Fórum de Matemática | DÚVIDAS? Nós respondemos!
https://forumdematematica.org/

Dúvidas Cônicas: Elipse, Hipérbole e Parábola :|
https://forumdematematica.org/viewtopic.php?f=23&t=3062		 Página 1 de 1
Autor:  Hellen Queiroz [ 07 jul 2013, 18:51 ]
Título da Pergunta:  Dúvidas Cônicas: Elipse, Hipérbole e Parábola :|
:( Boa noite pessoal, estou tendo dificuldade nesses exercícios pois o professor mandou estudar nas férias Cônicas: elipse, hipérbole e parábola e agora estou tentando resolvê-los, já fiz outros, mas essas eu não sei, faço o 3º ano do ensino médio e preciso saber fazer essas questões para conseguir fazer a prova na segunda que vem, e os exercícios serão parecidos, mas se eu não souber fazer este não saberei fazer os da prova, não sei nem por onde ir, fiz a primeira letra A e deu (x-6)²/9 + (y-7)²/39=1, mas poderiam confirmar por favor? Já li em sites e não consigo entender. Estou tão desesperada que vim parar aqui, desculpem o incomodo, se alguém quiser me explicar eu aceito.
Eu só tenho horário livre pela noite, no resto do dia trabalho, as férias só foram de 2 semanas e desde então venho fazendo vários exercícios mas que não são parecidos com esses aí.

Anexos:
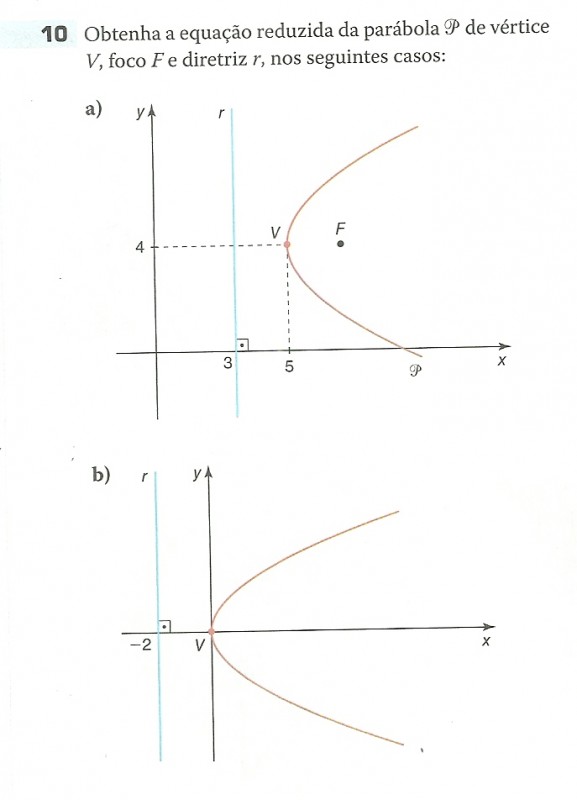
digitalizar0005.jpg
digitalizar0005.jpg [ 81.42 KiB | Visualizado 3170 vezes ]
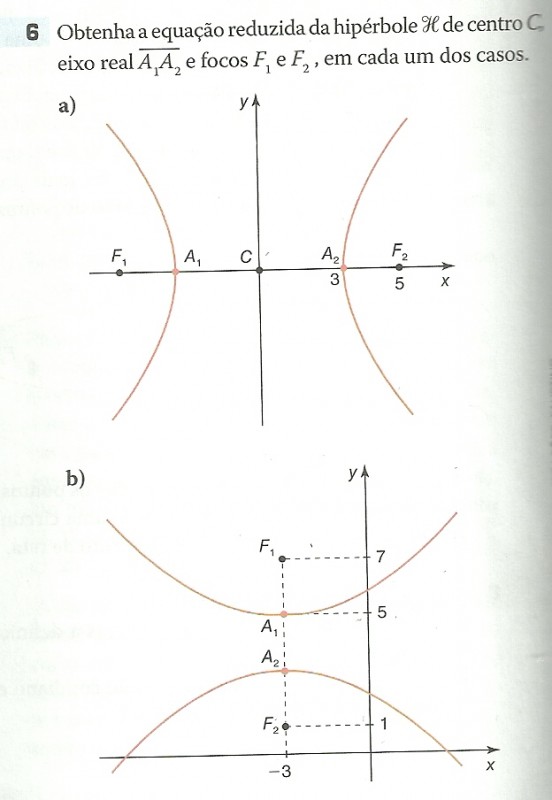
digitalizar0004.jpg
digitalizar0004.jpg [ 119.27 KiB | Visualizado 3170 vezes ]
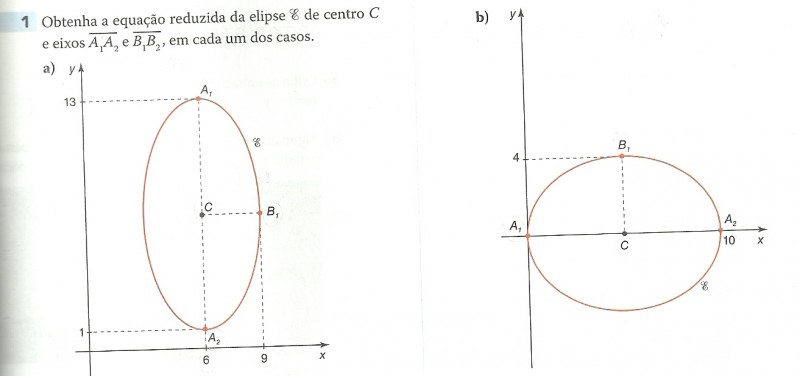
digitalizar0003.jpg
digitalizar0003.jpg [ 128.88 KiB | Visualizado 3172 vezes ]
Autor:  Hellen Queiroz [ 08 jul 2013, 14:22 ]
Título da Pergunta:  Re: Dúvidas revisão de Cônicas, Elipe e Hipérbole
Pessoal me ajudem por favor, estou desesperada, ninguém me ajuda, isso é só para eu ter como base algo para fazer a prova, eu mal tenho tempo para estudar, mas alguém me ajudando hoje mesmo antes da aula tentarei refazer e ver se consigo, não custa nada, eu tentarei ajudar-los em outros problemas pelos quais eu sei fazer, é uma troca. Faz semanas que estudo esse assunto, mas o meu fraco é equação reduzida.
Autor:  Fraol [ 09 jul 2013, 02:16 ]
Título da Pergunta:  Re: Dúvidas Cônicas: Elipe, Hipérbole e Parábola :|
Boa noite,

Essas equações são difíceis de lembrar, mas não tem muito jeito caso contrário é necessário deduzir e isso pode levar tempo, ainda mais numa prova. Por falar em tempo, espero que não seja tarde demais para alguma ajuda.

No caso da parábola horizontal (grifo meu) com com concavidade para a direita e vértice \(V=(x_V, y_V)\), a fórmula da equação reduzida é:

\((y-y_V)^2 = 2p(x-x_V)\) onde p é o tal do parâmetro da parábola que nada mais é do que a distância do Foco à reta diretriz.

Colocando os valores conforme o problema 10a:
Nesse caso V=(5,4) e p=4 (por quê?)

\((y-4)^2 = 8(x-5)\)

O item b é análogo.
Autor:  Fraol [ 09 jul 2013, 02:28 ]
Título da Pergunta:  Re: Dúvidas Cônicas: Elipe, Hipérbole e Parábola :|
No caso da hipérbole vertical (grifo meu) de centro \(O=(x_O, y_O)\), a fórmula da equação reduzida é:

\(\frac{(x-x_O)^2}{a^2} - \frac{(y-y_O)^2}{b^2} = 1)\) onde \(a\) é a distância do centro a um dos vértices e \(b\) é a metade da medida do eixo conjugado (um eixo vertical que passa pelo centro). \(a\) e \(b\) são catetos de um triângulo retângulo cuja hipotenusa mede a distância entre o centro e um dos focos.

Colocando os valores conforme o problema 6a:
Nesse caso O=C=(0,0) e a=3 e b=4 (por quê?)

\(\frac{(x)^2}{3^2} - \frac{(y)^2}{4^2} = 1)\)

O item b é análogo (deve-se trocar x por y ) .
Autor:  npl [ 09 jul 2013, 10:01 ]
Título da Pergunta:  Decorar, não as fórmulas mas as ideias
Cara Hellen Queiroz

As fórmulas das cónicas têm ideias que as sustentam que levaram à dedução das respectivas fórmulas.
Eu "nunca" sei fórmulas de cor, ou melhor, evito ao máximo decorar (matemática).
Sabendo as ideias quando preciso deduzo as fórmulas em causa. Funciona e nunca se esquece...

Assim para Parábola só tem que ter em mente que esta representa o conjunto de pontos que estão a igual distância dum ponto e duma recta dadas.
No caso que refere só deverá considerar como variável dependente X e como independente Y.
Subtrair o deslocamento da variável Y(a altura do foco) à sua variável independente(Y) e adicionar ao resultado(variável dependente, isto é, X)a abcissa do ponto médio da distância entre o foco e a recta.
A partir daqui será tudo muito linear. Experimente e questione-me novamente se encontrar dificuldades.


No caso da Hipérbole terá que ter em mente que esta representa o conjunto de pontos cuja diferença das distâncias aos dois focos(pontos) dados é constante. Tenho ideia que a sua dedução implica um pouco mais de habilidade mas aqui vai a fórmula de qualquer forma que ainda me lembro de cor:
\(ax^2-by^2=1\)

\(a\) e \(b\) representam(salvo erro/se a memória não me falha) a largura e altura(não necessariamente por esta ordem), isto é o declive do triângulo rectângulo associado às directrizes da hipérbole.
Terá que ver qual das variáveis deve considerar livre consoante a rotação da Hipérbole. A maneira de compreender esse \(a\) e \(b\) é ter em mente quando X(ou Y) valem zero o resultado da equação tem que respeitar essa diferença constante, que é a ideia base para a dedução da fórmula da hipérbole.

Por último a ideia associada ao conjunto de pontos que formam uma elipse é a da soma das distâncias dos pontos aos dois focos dados ser constante. Se se lembrar da fórmula da circunferência(caso particular das elipses com excentricidade 1) só terá que juntar dois coeficientes(multiplicadores) que deformaram a sua circunferência para obter a elipse propriamente dita. Para não andar a decorar fórmulas o melhor é mesmo aprender a deduzi-las.
A fórmula é a seguinte:

\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(a\) e \(b\) representam o máximo afastamento ortogonal que os pontos da elipse atingem relativamente à origem do referencial.
Substitua na fórmula \(x\) e \(y\) pelas constantes em causa \(a\) e \(b\) e veja o resultado que a fórmula produz!

PS - Naturalmente terá que ajustar(deslocar/subtrair) os valores das variáveis \(x\) e \(y\) de constantes que representarão a distância do centro da elipse à origem do referencial se este não for o centro da elipse! Isso já tinha sido tomado em conta nas fórmulas dos posts mais acima.
Autor:  npl [ 11 jul 2013, 11:48 ]
Título da Pergunta:  Thread repetido
2 posts para as mesmas questões...

viewtopic.php?f=14&t=3070
Autor:  Hellen Queiroz [ 15 jul 2013, 14:36 ]
Título da Pergunta:  Re: Dúvidas Cônicas: Elipse, Hipérbole e Parábola :|
Obrigada pessoal, e me perdoem, não tinha parado para ler as regras, não farei isso da próxima vez
Página 1 de 1 Os Horários são TMG [ DST ]
Powered by phpBB® Forum Software © phpBB Group
https://www.phpbb.com/