| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Volume de um prisma oblíıquo. https://forumdematematica.org/viewtopic.php?f=23&t=5733 |
Página 1 de 1 |
| Autor: | Gonsalves [ 13 abr 2014, 14:40 ] |
| Título da Pergunta: | Volume de um prisma oblíıquo. |
Alguém sabe esta? Determine o volume de um prisma oblíquo, sabendo que a base é um quadrado de lado com 7 cm de comprimento, e que a aresta lateral mede 4 cm e forma com o plano da base um ângulo de 45 graus. |
|
| Autor: | João P. Ferreira [ 15 abr 2014, 09:40 ] | ||
| Título da Pergunta: | Re: Volume de um prisma oblíıquo. | ||
isso é muito semelhante a calcular a área de um paralelograma http://pt.wikipedia.org/wiki/Paralelogramo o seu paralelegrama terá um lado igual a 7cm e outro igual a 4 cm depois da saber essa área é só multiplicar pela profunidade (4cm) e obtem o volume PS: amigo, não precisa de gritar, não somos cegos 
|
|||
| Autor: | Gonsalves [ 16 abr 2014, 01:23 ] |
| Título da Pergunta: | Re: Volume de um prisma oblíıquo. |
Não entendi. E esses 45 graus não vai me servir de nada? |
|
| Autor: | Kito [ 16 abr 2014, 01:34 ] |
| Título da Pergunta: | Re: Volume de um prisma oblíıquo. |
João, Poderia nos demonstrar como seria a resolução desse exercício. Fiquei confuso com o enunciado. Obrigado. |
|
| Autor: | Sobolev [ 16 abr 2014, 11:24 ] | ||
| Título da Pergunta: | Re: Volume de um prisma oblíıquo. | ||
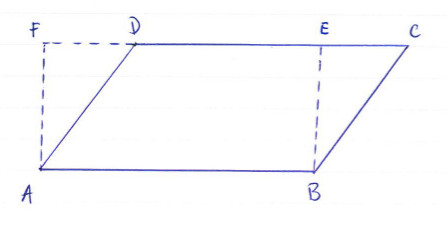
A imagem representa o prisma, visto de frente, tal como sugeriu o João Ferreira. Repare que os triangulos [ADF] e [BCE] são exactamente iguais, pelo que a área do paralelogramo [ABCD] é igual à do rectângulo [ABEF]. O valor do ângulo de 45º é importante pois é o que permite calcular \(\bar{BE}= 2 \sqrt{2}\). Deste modo vê que a área do paralelogramo é \(7 \times 2 \sqrt{2} = 14 \sqrt{2}\). Finalmente, o volume é obtido multiplicando a valor da área pela profundidade, que resulta na resposta final de \(7 \times 14 \sqrt{2} = 98 \sqrt{2}\). OBS. \(\bar{AB} = \bar{DC} = \mathrm{7} \bar{AD}=\bar{BC} = \mathrm{4} \bar{BE} = \bar{BC} \cos \frac{\pi}{4} = 4 \sqrt{2}/2 = \mathrm{2} \sqrt{2}\)
|
|||
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|