| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Altura e área do tronco de pirâmide quadrangular https://forumdematematica.org/viewtopic.php?f=23&t=6955 |
Página 1 de 1 |
| Autor: | martor314 [ 21 set 2014, 13:22 ] |
| Título da Pergunta: | Altura e área do tronco de pirâmide quadrangular |
Um tronco de pirâmide quadrangular regular possui diagonal da base maior com 12√2 cm e aresta da base menor com 4 cm. A partir das informações apresentadas, determine a: a) Altura do tronco da pirâmide b) área lateral c) área total Gabarito: a) 4 cm b) 128√2 cm² c) 32(4√2+5) cm² A imagem da pirâmide Anexo: IMG_20140921_091130_779[1].jpg [ 1.33 MiB | Visualizado 2931 vezes ] Grato. |
|
| Autor: | TelmaG [ 26 dez 2014, 23:14 ] | ||
| Título da Pergunta: | Re: Altura e área do tronco de pirâmide quadrangular | ||
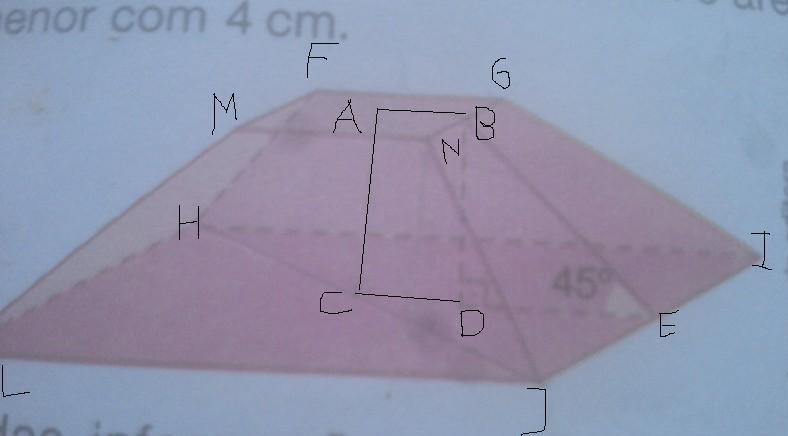
a) Considerando o triângulo [H L J] e sabendo que é retângulo em L pela fórmula do Teorema de Pitágoras podemos determinar: como a base HILJ é um quadrado vem HL= LJ= x então: (12√2_)^2= HL^2 + LJ^2 <=> (12√2_)^2=2x^2 <=> x= √(144.2/2) <=> x= 12 Por outro lado, CE= HI/2 <=> CE= 6 e AB= FG/2 <=> AB= 2 e CD= AB então CE - CD= 4 Como o triângulo [B D E] tem o ângulo BDE= 90º e o ângulo BED= 45º tem de ter o ângulo DBE= 45º logo trata-se de um triângulo isósceles onde: BD= DE= 4 Por fim, AC que é a altura do tronco da pirâmide é igual a BD. Assim, a altura é igual a 4 cm como queríamos demonstrar. b) Cálculo de BE: BE^2= ND^2 + DE^2 <=> BE^2= 4^2 + 4^2 <=> BE= √32= 4√2 Atrapézio= (JI + NG)/2 . BE At= (12+4)/2 x 4√2 <=> At= 32√2 e Al= 4At logo Al= 128√2 c) ATotal= Al + Abasemaior + Abasemenor AT= 128√2 + 12^2 + 4^2 <=> AT= 128√2 + 160 cm² *Nota: o número máximo pelo qual podemos dividir simultaneamente 128 e 160 é 32. Assim pondo 32 em evidência temos: AT= 32( 4√2 + 5) cm²
|
|||
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|