| Fórum de Matemática | DÚVIDAS? Nós respondemos! https://forumdematematica.org/ |
|
| Triangulos em zigue-zague resolução https://forumdematematica.org/viewtopic.php?f=23&t=9810 |
Página 1 de 1 |
| Autor: | Bruno Reagan [ 02 nov 2015, 18:33 ] | ||
| Título da Pergunta: | Triangulos em zigue-zague resolução | ||
Olá!! Há certo tempo tenho tentado resolver o exercício que segue, mas não encontro um raciocínio ou linha para seguir e achar a economia de pano proporcionada. Poderiam me indicar como prosseguir. Segue a foto do exercício.
|
|||
| Autor: | Baltuilhe [ 03 nov 2015, 01:19 ] |
| Título da Pergunta: | Re: Triangulos em zigue-zague resolução [resolvida] |
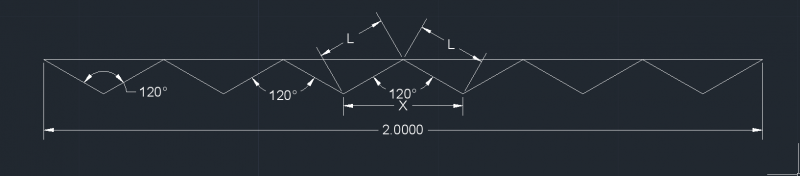
Boa noite! Anexo: Captura de Tela 2015-11-02 às 21.14.38.png [ 28.19 KiB | Visualizado 1452 vezes ] Veja que cada dobra da cortina (a parte em V) será substituída por uma parte reta. Se analisarmos este triângulo verá que tem um ângulo de 120º e dois lados iguais a L (não nos importa o tamanho, ok?). Se aplicarmos a lei dos cossenos podemos calcular o valor de X. \(X^2=L^2+L^2-2LL\cos{120^{\circ}} X^2=2L^2-2L^2\cos{-60^{\circ}} X^2=2L^2-2L^2(-\cos{60^{\circ}}) X^2=2L^2+2L^2\cos{60^{\circ}} X^2=2L^2+2L^2\frac{1}{2} X^2=2L^2+L^2=3L^2 X=L\sqrt{3}\) Agora podemos calcular o que se pede, já que temos 6 segmentos iguais a X substituindo 12 segmentos iguais a L, certo? O ganho em porcentagem é: \(\frac{X-2L}{2L}=\frac{L\sqrt{3}-2L}{2L}=\frac{1,7L-2L}{2L}=\frac{0,3L}{2L}=0,15=15\%\) Então, a economia será entre 11% e 15%. Espero ter ajudado! |
|
| Autor: | Bruno Reagan [ 03 nov 2015, 18:23 ] |
| Título da Pergunta: | Re: Triangulos em zigue-zague resolução |
Obrigado por sua ajuda, Baltuilhe! Logo entendi seu raciocínio. Valeu 
|
|
| Autor: | Baltuilhe [ 03 nov 2015, 22:40 ] |
| Título da Pergunta: | Re: Triangulos em zigue-zague resolução |
Boa tarde! Fiz uma correção onde esqueci-me de iniciar o código no LATEX ! Deve ter ficado mais legível, agora! Abraços! |
|
| Página 1 de 1 | Os Horários são TMG [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|