|
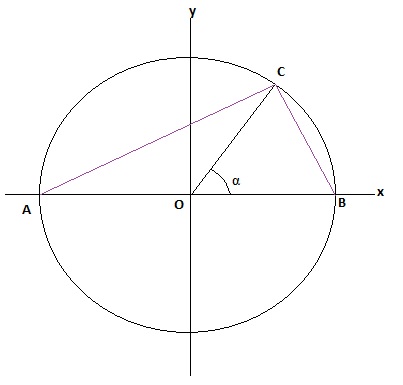
Enunciado: A figura mostra a circunferência trigonométrica, cujo raio mede 1, e o triângulo ABC, de área 2/3, inscrito na circunferência.
Bom pessoal, primeiramente segue a imagem do exercício e, em seguida, os meus registro sobre o exercício em uma segunda figura.
Minha resolução
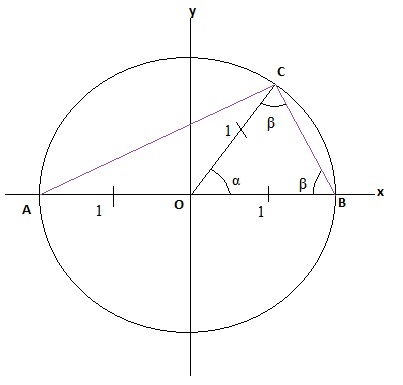
Observa-se que o ângulo em C é retângulo, mas isso não será útil.
No triângulo ABC, tem-se
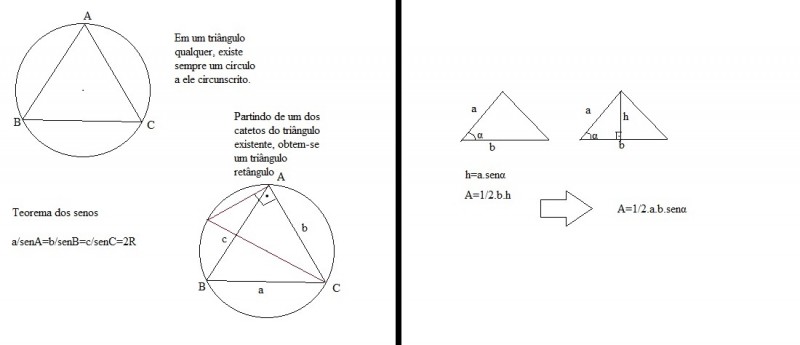
\(A=\frac{1}{2}.a.b.sen.\beta\)
\(\frac{2}{3}=\frac{1}{2}.2.BC.sen.\beta\)
\(sen\beta =\frac{2}{3.BC}\)
Porém, pelo teorema dos senos no triângulo isósceles OBC
\(\frac{1}{sen\beta }=\frac{BC}{sen\alpha }\)
\(sen\beta =\frac{sen\alpha }{BC}\)
Igualando as duas expressões, vem
\(\frac{2}{3BC}=\frac{sen\alpha }{BC}\)
\(sen\alpha =\frac{2}{3}\)
Pela relação fundamental da trigonometria
\(sen^2\alpha +cos^2\alpha =1\)
\(cos^2\alpha =1-sen^2\alpha\)
\(cos^2\alpha =1-(\frac{2}{3})^2\)
\(cos^2\alpha =1-\frac{4}{9}\)
\(cos^2\alpha =\frac{9}{9}-\frac{4}{9}\)
\(cos^2\alpha =\frac{5}{9}\)
\(cos\alpha =\sqrt{\frac{5}{9}}\)
O valor negativo não deve ser considerado, pois o ângulo se encontra no primeiro quadrante, onde o cosseno adquire valores positivos. O resultado pode ser simplificado para "raiz de cinco sobre três", mas não consegui separar o membro antecedente do membro consequente no LaTeX. Ignorância minha.
Em anexo, também coloquei as deduções das propriedades que utilizei, com exceção da fundamental que ainda não aprendi a deduzir. Isto é para a informação de quem estiver interessado em aprender e para exercitar as deduções, aprendendo mais também. Ainda, enriquece o tópico, é claro.
Contudo, em relação ao exercício, gostaria de saber se ele está correto e se existe outro modo de chegar na resposta. Existe a alternativa "raiz de cinco sobre três" nas respostas, mas não tenho o gabarito.
Grato.
| Anexos: |
Teorema dos senos e área.jpg [ 58.73 KiB | Visualizado 5173 vezes ]
|
Minha resolução.jpg [ 19.34 KiB | Visualizado 5173 vezes ]
|
Exercício.jpg [ 17.83 KiB | Visualizado 5174 vezes ]
|
|

