Fórum de Matemática
DÚVIDAS? Nós respondemos!

No dia do Círio de N. S. de Nazaré, a diretora de uma Escola Municipal reuniu 40 professores e ofereceu um almoço, tendo como pratos principais o pato no tucupi e a maniçoba. Desses professores,1/4 comeu só pato no tucupi ,3/10 só maniçoba e 1/5 , os dois. Quantos não comeram nem pato nem maniçoba?

Este exercício pode ser resolvido recorrendo à axiomática da probabilidade:

consideremos como acontecimentos em questão os acontecimentos A e B, e que:

A - comer pato no tucupi
B - comer maniçoba

nesse caso, as probabilidades dadas são, respetivamente, p(A)=1/4, p(B)=3/10 e \(p(A\cap B)=\frac{1}{5}\)
e o que pretendem é \(N\times p(\bar{A}\cap \bar{B})\), em que N é o número de professores que participam no almoço, ou seja, N=40.

pela axiomática das probabilidades (nomeadamente leis de DeMorgan), é possível desenvolver a probabilidade pedida de modo a calculá-la à custa das restantes dadas, ou seja:

\(p(\bar{A}\cap \bar{B})=p(\overline{A\cup B})=1-p(A\cup B)=1-\left [ p(A)+p(B)-p(A\cap B) \right ]=1-\frac{1}{4}-\frac{3}{10}+\frac{1}{5}=\frac{13}{20}\)

Para saber quantos professores efetivamente não comeram um prato nem o outro, basta multiplicar a probabilidade pelo nº de professores, obtendo-se 26 professores.

A resposta anterior embora tenha o raciocínio correto, na minha opinião está errada, porque houve um lapso na interpretação do problema.

A - comer pato no tucupi
B - comer maniçoba



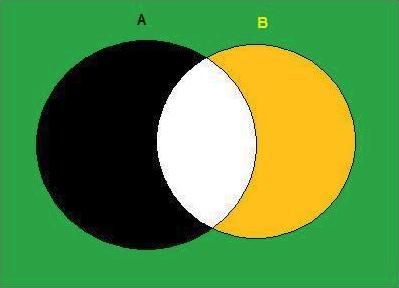
Segundo o enunciado do problema, 1/4 dos professores comeu só pato no tucupi (no diagrama de Veen disponibilizado em cima, a parte do conjunto A que se refere apenas ao pato no tucupi está pintada a preto, uma vez que se tem de excluir aqueles professores que comeram ambos os pratos, ou seja, exclui-se a intersecção do conjunto A com o conjunto B assinalada a branco no diagrama. Do mesmo modo, 3/10 corresponde aos professores que comeram só maniçoba (parte do conjunto B pintada a amarelo), porque corresponde ao conjunto B menos a intersecção.
Então recorrendo à axiomática de probabilidades temos:
\(P(A\cap \overline{B})=\frac{1}{4}\; e\; P(\overline{A}\cap B)=\frac{3}{10}\; e\; P(A\cap B)=\frac{1}{5}\)

Com o auxílio de um diagrama podemos deduzir:
\(P(A\cap \overline{B})=P(A)-P(A\cap B)\; e\; P(\overline{A}\cap B)=P(B)-P(A\cap B)\)

Assim, podemos substituir os valores dados no enunciado em cada equação:
\(P(A)=P(A\cap \overline{B})+P(A\cap B)=\frac{1}{4}+\frac{1}{5}=\frac{9}{20}\; e\; P(B)=P(\overline{A}\cap B)+P(A\cap B)=\frac{3}{10}+\frac{1}{5}=\frac{1}{2}\)

Agora podemos recorrer à equação já estabelecida \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\) e substituir os valores obtidos anteriormente:
\(P(A\cup B)=\frac{9}{20}+\frac{1}{2}-\frac{1}{5}=\frac{3}{4}\)

Como pretendemos saber o número de professores que não comeu nenhum dos dois pratos, utilizamos a expressão \(1-P(A\cup B)=1-\frac{3}{4}=\frac{1}{4}\), ou seja, 1/4 do total de professores não comeu nem pato no tucupi nem maniçoba (no diagrama de Venn está assinalado a verde). Portanto, (1/4)x40= 10. Resposta final: 10 professores

Podíamos também resolver o problema por um método mais simples:
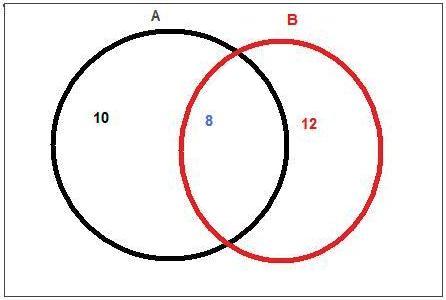
(1/4)x40=10 professores que só comeram pato no tucupi
(3/10)x40= 12 professores que só comeram maniçoba
(1/5)x40= 8 professores que comeram ambos os pratos


Podemos somar o número de professores que só comeu pato no tucupi ao número de profs. que só comeu maniçoba e, por sua vez, ao número de profs. que comeu ambos os pratos (e por isso comum aos dois conjuntos), obtendo o número de professores que comeram pelo menos um dos pratos. Se ao total de 40 subtrairmos o valor obtido chegamos ao valor de 10, ou seja, àqueles que não comeram nenhum dos pratos referidos.

Como disse no início, esta é só a minha opinião e não garanto que esteja certa, mas pelo menos é assim que eu resolveria o problema.

Tem razão, de facto estive a ler o exercício novamente e dizem que os professores comeram "só" um prato ou "só" o outro, o que quer dizer que tem que se excluir a interseção. Muito obrigada pela correção e peço desculpa a ambos pelo lapso na leitura!